En nuestros tiempos de avances tecnológicos es necesario y casi prioritario el uso de cálculos y funciones que a pesar que fueron creadas hace mucho tiempo siempre van a ser información y material de importancia en el moderno mundo de hoy
Historia del teorema del seno y el coseno:
Los Elementos de Euclides, que datan del siglo III a. C., contienen ya una aproximación geométrica de la generalización del teorema de Pitágoras .La formulación de la época es arcaica ya que la ausencia de funciones trigonométricas y del álgebra obligó a razonar en términos de diferencias de áreas. Por esto se comienzan a utilizar los siguientes términos:
«En los triángulos obtusángulos, el cuadrado del lado opuesto al ángulo obtuso es mayor que los cuadrados de los lados que comprenden el ángulo obtuso en dos veces el rectángulo comprendido por un lado de los del ángulo obtuso sobre el que cae la perpendicular y la recta exterior cortada por la perpendicular, hasta el ángulo obtuso.»
Faltaba esperar la trigonometría árabe-musulmana de la Edad Media para ver al teorema evolucionar a su forma y en su alcance: el astrónomo y matemático al-Battani generalizó el resultado de Euclides en la geometría esférica a principios del siglo X, lo que permitió efectuar los cálculos de la distancia angular entre el Sol y la Tierra. Fue durante el mismo período cuando se establecieron las primeras tablas trigonométricas, para las funciones seno y coseno. Eso permitió a Ghiyath al-Kashi, matemático de la escuela de Samarcanda, de poner el teorema bajo una forma utilizable para la triangulación durante el siglo XV. La propiedad fue popularizada en occidente por François Viète quien, al parecer, lo redescubrió independientemente.
Fue a finales del siglo XVII cuando la notación algebraica moderna, aunada a la notación moderna de las funciones trigonométricas introducida por Euler en su libro Introductio in analysin infinitorum, permitieron escribir el teorema bajo su forma actual, extendiéndose el nombre de teorema (o ley) del coseno.
Ley del seno:
Un triángulo oblicuo es aquel que no tiene un ángulo recto. Usaremos la literales A, B, C, a, b, c ,α,β, λ, para distinguir partes de los triángulos.
Supongamos que ABC es un triangulo oblicuo con los angulos y lados marcados en la forma acostumbrada:
Entonces:
observa que la ley de los senos consta de los senos consta de las siguientes tres formulas:
para aplicar cualquiera de estas fórmulas a un triangulo especifico debemos conocer los valores de tres de las cuatro variables. Si sustituyes estos tres valores en la forma apropiada, podrás despejar el valor de la cuarta variable.
Se deduce que la ley de los senos se puede hallar las partes restantes de un triangulo oblicuo, siempre que se conozcan cualquiera de las siguientes dos condiciones (las tres letras dentro del paréntesis significan las partes conocidas con "L" representando un lado y "A" ángulo) :
1) dos lados y un ángulo opuesto a uno de ellos (LLA)
2) dos ángulos y cualquier lado (AAL) o (ALA) en la sección siguiente estudiaremos la ley de los cosenos y y demostraremos como se usa para hallar las partes restantes del triángulo oblicuo cuando se conoce los siguiente:
1) dos lados y el triangulo entre ellos (LAL)
2) tres lados (LLL)
La ley de los senos no se puede aplicar directamente a los dos últimos casos. Esta ley también se puede escribir en la forma.
en lugar de memorizar las tres fórmulas relacionadas con la ley de los senos. Pueden ser mas conveniente recordar el siguiente enunciado, que toma en cuenta a todas ellas.
Ley de los senos: en cualquier triángulo, la razón entre el seno de un ángulo y el lado opuesto a ese ángulo es igual a la razón entre el seno de otro ángulo y el lado opuesto a ese ángulo.
Ejemplo: Cuando el ángulo de elevación del sol es de 64°, un poste de teléfonos inclinado a un ángulo de de 9° en direccion opuesta al sol arroja una sombra de 21 pies de largo a nivel del suelo. Calcula la longitud del poste.
β = 90°- 9° = 81°
λ = 180
Para hallar la longitud del poste; es decir , el lado de α del triagulo ABC se procede como sigue:




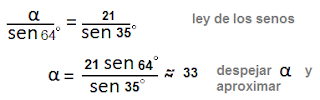
http://espanol.answers.yahoo.com/question/index?qid=20090318041030AAwM1mQ
ResponderEliminarMuy buena respuesta
ResponderEliminarde donde saco la historia del teorema del seno?
ResponderEliminar